Two lines are perpendicular if and only if:
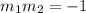
Then we need to find the slopes of each of them. We know that the slope-intercept form is:

Then, comparing the first equation with the general form we have that:
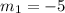
Now, to find the slope of the second equation we first solve it for y:
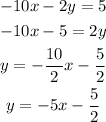
Then:
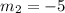
Now we make the product:
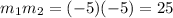
Since the slopes don't fullfil the condition we condlude that the lines are not perpendicular.