Question

Find a formula for the area of the grey triangle assume p is the centre of the smaller square

Answer 1

Since the gry triangle is the folded part of the paper which has dimensions

`\begin{gathered} L=x+y \\ W=x+(1)/(2)d(\text{small square)} \end{gathered}`

L is the length

x is the side of the small square

y is the side of the big square

d is the diagonal of the small square

The relation between the side of a square and its diagonal is

`d=s\sqrt[]{2}`

s is the side of the square

d is its diagonal

Since p Is the center of the small square, then

The side PQ = 1/2 the diagonal

Since the side of the small square is x, then its diagonal is

`d=x\sqrt[]{2}`

From here we know that

The base of the gry triangle is PQ which equal to

`\begin{gathered} PQ=(1)/(2)x\sqrt[]{2} \\ PQ=\frac{\sqrt[]{2}}{2}x \end{gathered}`

The height of the triangle RP is equal to the length of the unfolded figure which is

`RP=x+y`

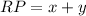
The formula of the area of a triangle is

`A=(1)/(2)bh`

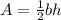
Substitute the base by PQ and the height by PR

`\begin{gathered} A=(1)/(2)(\frac{\sqrt[]{2}}{2}x)(x+y) \\ A=\frac{\sqrt[]{2}}{4}x(x+y) \end{gathered}`