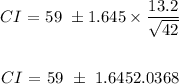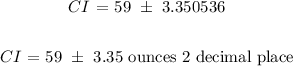Question

Question 12 pts 1 DetailsYou measure 42 turtles' weights, and find they have a mean weight of 59 ounces. Assume thepopulation standard deviation is 13.2 ounces. Based on this, construct a 90% confidence interval forthe true population mean turtle weight.Give your answers as decimals, to two places±ounces ?

Answer 1

Answer:
`CI\text{ = 59 }\pm\text{ 3.35 ounces}`

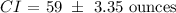
Step-by-step explanation:

Given:

number of turtles = 42

mean weight = 59 ounces

Population standard deviation = 13.2 ounces

To find:

To construct a 90% confidence interval for the true population mean

To get the confidence interval, we will apply the formula:

`\begin{gathered} CI\text{ = mean }\pm\text{ Z}_{90\text{ \%}}*(\sigma)/(√(n)) \\ \sigma\text{ = standard deviation} \\ n\text{ = number of sample} \end{gathered}`

Z score for 90% confidence interval = 1.645

`\begin{gathered} CI\text{ = 59 }\pm1.645*(13.2)/(√(42)) \\ \\ CI\text{ = 59 }\pm\text{ 1.645\lparen2.0368\rparen} \end{gathered}`
`\begin{gathered} CI\text{ = 59 }\pm\text{ 3.350536} \\ \\ CI\text{ = 59 }\pm\text{ 3.35 ounces \lparen2 decimal place\rparen} \end{gathered}`