Question

The volume of gas kept at a constant pressure varies inversely with the temperature T. If the temperature is 50 degrees, the volume is 20 cubic feet. What will the volume be when the temperature is 100 degrees. 1. Define variables. 2. Write an equation 3. Solution?

Answer 1

Volume V is inversely proportional to temperature T, when pressure is constant, then:

`V\propto(1)/(T)`

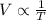
So, for a constant pressure P, we can create the following formula

`V=(P)/(T)\Rightarrow VT=P`

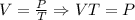
* If the temperature is 50 degrees, the volume is 20 cubic feet. What will the volume be when the temperature is 100 degrees.

Since P is mantain constant, then

`\begin{gathered} P=V_1T_1=V_2T_2 \\ \Rightarrow V_2=(V_1T_1)/(T_2) \end{gathered}`

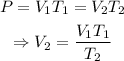
Where, the variables are:

V1 is the initial volume = 20 cubic feet

T1 is the initial temperatura = 50 degrees

V2 is the final volume in cubic feet

T2 is the final temperature = 100 degrees

Now, let's replace into the equation

`V_2=(20\cdot50)/(100)=(1000)/(100)=10`

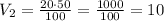
Thus, the solution is 10 cubic feet