Question

A toy manufacturer needs a piece of plastic in the shape of a right triangle with the longer leg 7 cm more than the shorter leg and the hypotenuse 14 cm more than the shorter leg. How long should the sides of the triangle be?

Answer 1

Given the information about the right triangle we have the following:

since we have that the longer leg is 7cm more than the shorter leg, then:

`b=a+7`

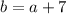
and also the hypotenuse is 14 cm more than the shorter leg, therefore:

`c=a+14`

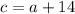
with these two expressions, we can find the value of the shorter leg:

`\begin{gathered} b=a+7 \\ c=a+14 \\ c^2=a^2+b^2 \\ \Rightarrow(a+14)^2=a^2+(a+7)^2 \\ \Rightarrow a^2+28a+196=a^2+a^2+14a+49 \\ \Rightarrow a^2+a^2+14a+49-a^2-28a-196=0 \\ \Rightarrow a^2-14a-147=0 \\ \Rightarrow(a-21)\cdot(a+7)=0 \end{gathered}`

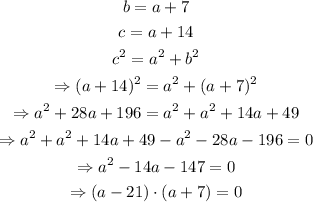
we have then that a=21 or a=-7. We choose a=21 since distances cannot be negative. Now we can find the value of b and c and check if they match using the pythagorean theorem again:

`\begin{gathered} a=21 \\ b=a+7=21+7=28 \\ c=a+14=21+14=32 \\ c^2=a^2+b^2 \\ \Rightarrow c^2=21^2+28^2=1225 \\ \Rightarrow c=\sqrt[]{1225}=35 \\ c=35 \end{gathered}`

therefore, the sides of the triangle should be 21 cm, 28 cm and 35 cm long