Question

I need help with all parts of this question please

Answer 1

Given,

The mass of the bullet, m₁=5 g=5×10⁻³ kg

The initial speed of the bullet, u=200 m/s

The mass of the block, m₂=2 kg

(a)

Given that the bullet will be embedded in the block after the collision. And the block was initially at rest which means that its initial momentum was zero.

From the law of conservation of momentum, the total momentum of the bullet-block system will remain the same after the collision as before the collision.

Thus,

`m_1u=(m_1+m_2)v`

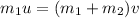
Where v is the velocity of the bullet and the block after the collision.

On substituting the known values in the above equation,

`\begin{gathered} 5*10^(-3)*200=(5*10^(-3)+2)v \\ \Rightarrow v=(5*10^(-3)*200)/((5*10^(-3)+2)) \\ =0.5\text{ m/s} \end{gathered}`

Thus the speed of the block and the bullet after the collision will be 0.5 m/s.

(b)

Total initial kinetic energy is given by,

`K_i=(1)/(2)m_1u^2`

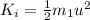
On substituting the known values,

`\begin{gathered} K_i=(1)/(2)*5*10^(-3)*200^2 \\ =100\text{ J} \end{gathered}`

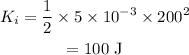
The kinetic energy of the system after the collision is given by,

`K_f=(1)/(2)(m_1+m_2)v^2_{}`

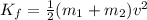
On substituting the known values,

`\begin{gathered} K_f=(1)/(2)*(5*10^(-3)+2)*0.5^2 \\ =0.25\text{ J} \end{gathered}`

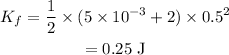
Thus the total kinetic energy lost during the collision is,

`\begin{gathered} \Delta K=K_i-K_f \\ =100-0.25 \\ =99.75\text{ J} \end{gathered}`

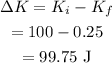
Thus the kinetic energy lost in the collision is 99.75 J

(c)

Given,

The speed of the bullet after it comes out from the other end of the block, v₁=100 m/s

From the law of conservation of energy, we have

`m_1u=m_1v_1+m_2v_2`

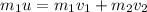
Where v₂ is the speed of the block of wood after the collision,

On substituting the known values,

`\begin{gathered} 5*10^(-3)*200=5*10^(-3)*100+2* v_2 \\ \Rightarrow v_2=(5*10^(-3)*200-5*10^(-3)*100)/(2) \\ =0.25\text{ m/s} \end{gathered}`

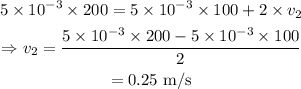
Thus the speed of the block after the collision in this given condition is 0.25 m/s.