Question

a bucket is filled at a consistent rate of 2.5 gallons per minute the book it will hold 18 gallons of water win for the volume v of water in the bucket is a function of T the time in minutes which is the best description of the domain of the function V

Answer 1

Given:

`\begin{gathered} consant\text{ rate = }2.5\text{ gallons/min} \\ bucket\text{ size = }18\text{ gallon} \end{gathered}`

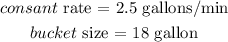
Let the time at which the bucket is filled be x

We can write:

At time t = 0 , Volume (V) = 0

At time t = x, Volume (V) = 18

Using the slope formula:

`\begin{gathered} \text{slope = }(V_(t=x)-V_(t=0))/(x-0) \\ (18-0)/(x-0)=\text{ 2.5} \end{gathered}`

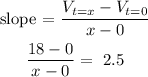
Solving for x:

`\begin{gathered} 2.5x\text{ = 18} \\ x\text{ = 7.2 min} \end{gathered}`

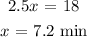
Recall that the domain of the function V is the time interval that satisfies the function.

Since the bucket becomes filled at 7.2min, the domain of the function V is:

`0\text{ }\leq\text{ t }\leq\text{ 7.2 }`

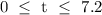
Answer: Option A