Given
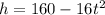
Where h is the height of the falling rock at time t, set h=0 and solve for t, as shown below
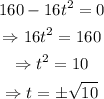
However, it is not possible that t<0 as it would imply that the rock reached the ground before falling; therefore, the only possible answer is t=sqrt(10).
Rounding the answer,
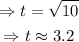
Hence, the answer is t=3.2