Question

At a table in the college cafeteria, three deans meet and discuss class size in their departments. The Math dean remarks, “It was kind of funny thing with our numbers. We divided all the students evenly among all the professors in the fall semester, and each class had exactly the same number of students. In the spring semester, we hired one additional professor and our student enrollment went up by exactly 1, and it turned out that our class size in the spring went down by exactly 1.”“Gee,” said the Biology dean, “We had something very similar happen. Like you, we divided all the students evenly among all the professors in the fall semester, and each class had exactly the same number of students. In the spring semester, we hired one additional professor and our student enrollment went up by exactly 1, and it turned out that our class size in the spring went down by exactly 2.”Then the History dean made his remarks: “You’re hardly going to believe this, but we divided all the students evenly among all the professors in the fall semester, and each class had exactly the same number of students. In the spring semester, we hired one additional professor and our student enrollment went up by exactly 1, and it turned out that our class size in the spring went down by exactly 3.”How many professors and students were there in the fall and spring in math, biology and history?

Answer 1

First, let's define our variables.

Let:

• M, be the number of ,math, teachers and ,m, be the number of math students.

,

• B, be the number of ,biology, teachers and ,b, be the number of ,biology, students.

,

• H, be the number of ,history, teachers and ,h, be the number of ,history, students.

Similarly, we'll have that:

• Cm, will be the number of students in a ,math, class.

,

• Cb, will be the number of students in a ,biology, class.

,

• Ch, will be the number of students in a ,history, class.

Now, we'll traslate what each dean said into mathematic expressions, so we can work on them and get our solution.

FOR MATH:

The dean said:

1. "We divided all the students evenly among all the professors in the fall semester, and each class had exactly the same number of students."

`(m)/(M)=C_m`

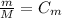
2. "In the spring semester, we hired one additional professor and our student enrollment went up by exactly 1, and it turned out that our class size in the spring went down by exactly 1.”

`(m+1)/(M+1)=C_m-1`

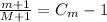
Now, let's clear Cm from equation 2 and equal both equations, as following:

`\begin{gathered} (m+1)/(M+1)=C_m-1 \\ \\ \rightarrow1+(m+1)/(M+1)=C_m \\ \\ \Rightarrow1+(m+1)/(M+1)=(m)/(M) \end{gathered}`

Solving for m, we'll get an expression for the number of students asigned to a certain number of teachers:

`\begin{gathered} 1+(m+1)/(M+1)=(m)/(M) \\ \\ \rightarrow(M+1+m+1)/(M+1)=(m)/(M)\rightarrow(M+m+2)/(M+1)=(m)/(M) \\ \\ M(M+m+2)=m(M+1) \\ \rightarrow M^2+Mm+2M=Mm+m \\ \rightarrow M^2+2M=m \\ \\ \Rightarrow m=M^2+2M \end{gathered}`

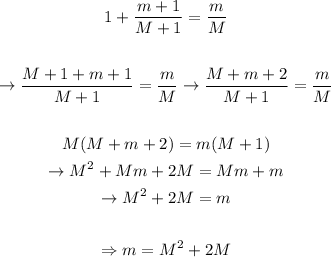
Now, we can choose any number of teachers that we want, and we'll get the corresponding number of students that make the dean's statements correct.

For instance, we can choose 10 teachers, and we'll get that:

• There were 10 teachers and 120 students in the fall semester

,

• There were 11 teachers and 121 students in the fall semester

FOR BIOLOGY:

The dean said:

1. "...we divided all the students evenly among all the professors in the fall semester, and each class had exactly the same number of students."

`(b)/(B)=C_b`

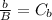
2. "In the spring semester, we hired one additional professor and our student enrollment went up by exactly 1, and it turned out that our class size in the spring went down by exactly 2."

`(b+1)/(B+1)=C_b-2`

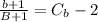
Similarly, we'll clear Cb from equation 2 and equal both equations, as following:

`\begin{gathered} (b+1)/(B+1)=C_b-2 \\ \\ \rightarrow2+(b+1)/(B+1)=C_b \\ \\ \Rightarrow2+(b+1)/(B+1)=(b)/(B) \end{gathered}`

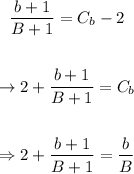
Solving for b, we'll get an expression for the number of students asigned to a certain number of teachers:

`\begin{gathered} 2+(b+1)/(B+1)=(b)/(B) \\ \\ \rightarrow(2B+2+b+1)/(B+1)=(b)/(B)\rightarrow(2B+b+3)/(B+1)=(b)/(B) \\ \\ \rightarrow B(2B+b+3)=b(B+1) \\ \rightarrow2B^2+Bb+3B=Bb+b \\ \rightarrow2B^2+3B=b \\ \\ \Rightarrow b=2B^2+3B \end{gathered}`

Now, we can choose any number of teachers that we want, and we'll get the corresponding number of students that make the dean's statements correct.

For instance, we can choose 10 teachers, and we'll get that:

• There were 10 teachers and 230 students in the fall semester

,

• There were 11 teachers and 231 students in the fall semester

FOR HISTORY:

The dean said:

1. "...we divided all the students evenly among all the professors in the fall semester, and each class had exactly the same number of students."

`(h)/(H)=C_h`

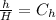
2. "In the spring semester, we hired one additional professor and our student enrollment went up by exactly 1, and it turned out that our class size in the spring went down by exactly 3."

`(h+1)/(H+1)=C_h-3`

Just as we did, we'll clear Ch from equation 2 and equal both equations, as following:

`\begin{gathered} (h+1)/(H+1)=C_h-3 \\ \\ \rightarrow3+(h+1)/(H+1)=C_h \\ \\ \Rightarrow3+(h+1)/(H+1)=(h)/(H) \end{gathered}`

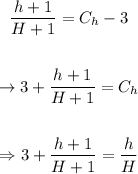
Solving for h, we'll get an expression for the number of students asigned to a certain number of teachers:

`\begin{gathered} 3+(h+1)/(H+1)=(h)/(H) \\ \\ \rightarrow(3H+3+h+1)/(H+1)=(h)/(H)\rightarrow(3H+h+4)/(H+1)=(h)/(H) \\ \\ \rightarrow H(3H+h+4)=h(H+1) \\ \rightarrow3H^2+hH+4H=hH+h \\ \rightarrow3H^2+4H=h \\ \\ \Rightarrow h=3H^2+4H \end{gathered}`

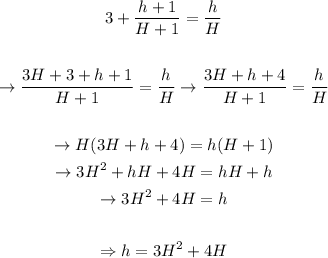
Now, we can choose any number of teachers that we want, and we'll get the corresponding number of students that make the dean's statements correct.

For instance, we can choose 10 teachers, and we'll get that:

• There were 10 teachers and 340 students in the fall semester

,

• There were 11 teachers and 341 students in the fall semester