Given:
The exponential function,
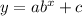
It passes through the points (0, 5) and (1, 14) and has a horizontal asymptote at y=2.
To find f(3):
Let us first find the values of a, b and c.
As we know, A function of the form
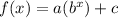
it always has a horizontal asymptote at y = c
So, substitute the point (0,5) and c = 2.
We get
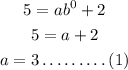
Substitute the point (1, 14), a=3 and c=2, we get
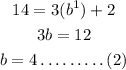
So, the given equation becomes,
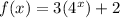
Next, substitute x=3, we get
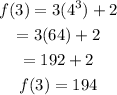
Hence, the solution is 194.