The Solution:
The coordinates of points A, B and C are
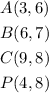
We are required to locate the images A', B', and C'
The difference between point A and its center of dilation, P, is

The difference between point B and its center of dilation, P, is
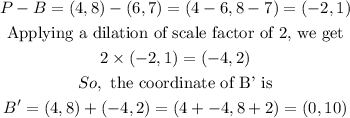
The difference between point C and its center of dilation, P, is
