We are asked to determine the amount of money necessary to be compounded semi-annually with an interest rate of 4 percent to get $15000 in three years. To do that we will use the following formula:

Where "A" is the future amount, "P" is the current amount, "r" is the interest rate in decimal notation, "n" is the number of times it is compounded and, "t" is the time.
Since it is compounded semi-annually this means that it is compounded twice a year, therefore n = 2. Replacing in the formula we get:
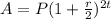
Now we solve for "P":
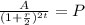
Now we replace the given values:
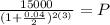
Solving the operations we get:
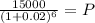
Solving the operations:
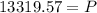
Therefore, the amount of money deposited must be $13319.57