ANSWER and EXPLANATION
A) We want to find the average rate of change of the function:
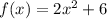
over the interval:

To do this, we apply the formula for the average rate of change of a function:

where (x₁, x₂) is the interval
Therefore, for the given function, we have that:

That is the average rate of change of the function over the given interval.
B) We found that the average rate of change of the function is 4.
The average rate of change of a function is a measure of how the output values of the function change with regard to its input values.
The average rate of change of the function is positive, which means that over the given interval, the function increases.
C) The function given is a quadratic function.
A quadratic function is known to increase and decrease over different intervals of x-values.
This means that the average rate of change of the function cannot be the same over all the intervals of x-values since the function is quadratic and its rate of change is a measure of the change (increase or decrease) of the function.