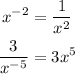Question

What are the first three laws of exponents?

Answer 1

Laws of Exponents

* Product. When multiplying like bases, keep the base the same and add the exponents. Example:

`x^3\cdot x^5=x^(3+5)=x^8`

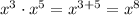
* Power to another power: When raising a base with a power to another power, keep the base the same and multiply the exponents. Example:

`(x^3)^5=x^(3\cdot5)=x^(15)`

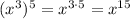
* Division: When dividing like bases, keep the base the same and subtract the denominator exponent from the numerator exponent. Example:

`(x^(14))/(x^4)=x^(14-4)=x^(10)`

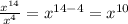
* Zero exponents: A real base raised to the exponent 0 is equal to 1. Examples:

`\begin{gathered} x^0=1 \\ 2^0=1 \end{gathered}`

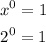
* Negative Power: When a negative exponent is used to raise a number, convert it to a reciprocal to make the exponent positive. Examples:

`\begin{gathered} x^(-2)=(1)/(x^2) \\ (3)/(x^(-5))=3x^5 \end{gathered}`