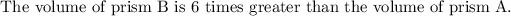Question

Given: rectangular prisms A and B. the length of Prism B is 3 times the length of Prism A. the width of Prism B is 4 times of width of Prism A. the height of Prism B is half of the height of Prism A. How many times is the volume of Prism B greater than Prism A?The volume of Prism B is

Answer 1

Given:

The length of Prism B is 3 times the length of Prism A. the width of Prism B is 4 times the width of Prism A. the height of Prism B is half of the height of Prism A.

Required:

We need to find the number of times the volume of Prism B is greater than Prism A.

Step-by-step explanation:

Let l be the length of Prism A.

Let w be the width of Prism A.

Let h be the height of Prism A.

The length of Prism B is 3 times the length of Prism A

`\text{ The length of Prism B =3l}`

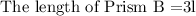
The width of Prism B is 4 times the width of Prism A.

`\text{ The width of Prism B =3w}`

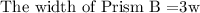
The height of Prism B is half of the height of Prism A.

`\text{ The height of Prism B =}(1)/(2)h`

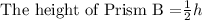
Consider the formula to find the value of the rectangular prism.

`Volume\text{ = length }* width* height`

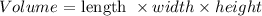
Substitute known values to find the volume of A.

`\text{ The volume of A=lwh}`

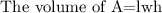
Substitute known values in the formula to find the volume of B.

`\text{ The volume of B=\lparen3l\rparen\lparen4w\rparen\lparen}(1)/(2)h)`

`\text{ The volume of B=6lw}h`

`Substitute\text{ the volume of A=lwh in the equation.}`

`\text{ The volume of B=6 times the volume of A.}`

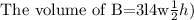
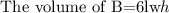
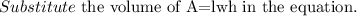
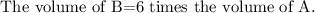
Final answer:

`\text{ The volume of prism B is 6 times greater than the volume of prism A.}`