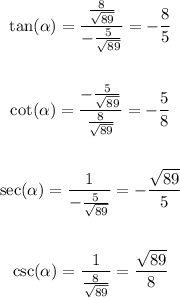Question

An angle A in standard position has a terminal side which passes through the point (-5,8)Determine the following Sin ACos A Tan ACot A Sec ACsc A

Answer 1

The points on the terminal side of an angle α can be described as:

`(r\cos(\alpha),r\sin(\alpha))`

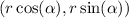
Where r is the distance from the origin to the point. Find r for the point (-5,8):

`r=√((-5)^2+(8)^2)=√(89)`

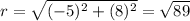
Then:

`\begin{gathered} √(89)\cos(\alpha)=-5\Rightarrow\cos(\alpha)=-(5)/(√(89)) \\ \\ √(89)\sin(\alpha)=8\Rightarrow\sin(\alpha)=(8)/(√(89)) \end{gathered}`

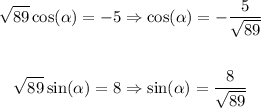
Recall the definitions of the tangent, cotangent, secant, and cosecant of an angle in terms of its sine and its cosine:

`\begin{gathered} \tan(\alpha)=(\sin(\alpha))/(\cos(\alpha)) \\ \cot(\alpha)=(\cos(\alpha))/(\sin(\alpha)) \\ \sec(\alpha)=(1)/(\cos(\alpha)) \\ \csc(\alpha)=(1)/(\sin(\alpha)) \end{gathered}`

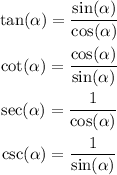
Replace the expressions for cos(α) and sin(α) to find the values of tan(α), cot(α), sec(α) and csc(α):

`\begin{gathered} \tan(\alpha)=((8)/(√(89)))/(-(5)/(√(89)))=-(8)/(5) \\ \\ \cot(\alpha)=(-(5)/(√(89)))/((8)/(√(89)))=-(5)/(8) \\ \\ \sec(\alpha)=(1)/(-(5)/(√(89)))=-(√(89))/(5) \\ \\ \csc(\alpha)=(1)/((8)/(√(89)))=(√(89))/(8) \end{gathered}`