Question

A student created this table to represent a linear relationship between x and y.X Y-2. 10.0-1. 7.50. 5.01. 2.52. 0 Part AWhat is the y-intercept of the line represented by the x and y values shownin the table? Show or explain how you got your answer.Enter your answer and your work or explanation in the space provided.

Answer 1

To find the equation of the line, we pick two corresponding points of x and y,

`\begin{gathered} (x_1,y_1)=(0,5.0) \\ (x_2,y_2)=(2,0) \end{gathered}`

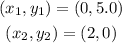
Formula to find the equation of a line is,

`(y-y_1)/(x-x_1)=(y_2-y_1)/(x_2-x_1)`

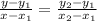
Substituting the points into the formula to find the equation of a line above,

Where the general equation of a straight line is given as,

`\begin{gathered} y=mx+c \\ \text{Where m is the slope and c is the y-intercept} \end{gathered}`
`\begin{gathered} \text{The equation of the line is,} \\ y=-(5)/(2)x+5 \end{gathered}`

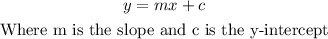
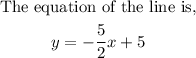
Comparing both equations, the c = 5, is the y-intercept.

Alternatively,

The y-intercept is the point where x = 0 and from the table provided,

Where x = 0, y = 5.

Hence, the y-intercept is 5.