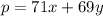
To be able to determine the corner point that gives us the maximum value in the objective function above, we simply have to plug in these possible points and see which one of the them gives us the highest value.
Let's start with option 1 (13, 0). In here, x = 13 and y = 0. Let's plug it in to the function and solve.

For option 1, the value of the function is 923.
Let's check option 2 at (10, 6). In here, x = 10 and y = 6.
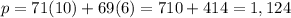
For Option 2, the value of the function is 1,124 and is higher than Option 1.
For Option 3, since it's (0, 0), the function is just equal to 0.
For Option 4, x = 8 and y = 5. Let's plug it in to the function.
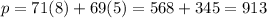
The value of the function in Option 4 is 913.
Lastly, for option 5, x = 0 and y = 11.
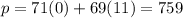
The value of the function in Option 5 is 759.
Out of the 5 options, the corner point at (10, 6) gave us the maximum value of 1,1,24. Hence, this point maximizes the objective function p = 71x + 69y.