Question

QuestionThe following data values represent the daily amount spent by a family during a 7 day summer vacation.Find the sample standard deviation of this dataset:$96, $125, $80, $110, $75, $100, $121Round the final answer to one decimal place.Provide your answer below:std

Answer 1

The dataset shown in the picture shows the daily amount spent by a family during a 7-day vacation.

The sample size is n=7

To calculate the standard deviation (S) you have to calculate its variance first. To calculate the sample variance (S²) you have to use the following formula:

`S^2=(1)/(n-1)\lbrack\Sigma x^2_i-((\Sigma x_i)^2)/(n)\rbrack`

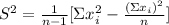
Before calculating the variance, you have to calculate the sum of the observations (∑xi) and the sum of squares of the observations (∑xi²)

`\begin{gathered} \Sigma x_i=96+125+80+110+75+100+121 \\ \Sigma x_i=707 \end{gathered}`
`\begin{gathered} \Sigma x^2_i=96^2+125^2+80^2+110^2+75^2+100^2+121^2 \\ \Sigma x^2_i=73607 \end{gathered}`

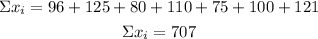
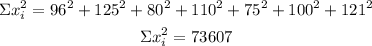
Replace both sums on the formula to determine the variance:

`\begin{gathered} S^2=(1)/(7-1)\lbrack73607-((707)^2)/(7)\rbrack \\ S^2=(1)/(6)\lbrack73607-71407\rbrack \\ S^2=(1)/(6)\cdot2200 \\ S^2=366.67 \end{gathered}`

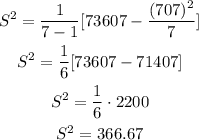
Once you have calculated the sample variance, to determine the sample standard deviation you have to calculate the square root of the variance:

`\begin{gathered} S=\sqrt[]{S^2} \\ S=\sqrt[]{366.67} \\ S=19.148 \\ S\approx19.1 \end{gathered}`

The standard deviation of the data set is S= $19.1