Question

119% of the population is 65 or older. Find the probability that the following number of persons selected at random from 25 people are 65 or olderThe probability that at most 2 are 65 or older is(Round to three decimal places as needed)

Answer 1

To solve the problem we will use the probability function of the binomial distribution, also called the Bernoulli distribution function, is expressed with the formula:

`P(x)=(n!)/((n-x)!\cdot x!)\cdot p^x\cdot q^(n-x)`

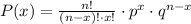
Where:

• n, ,=, the number of trials

,

• x, = the number of successes desired

,

• p, = probability of getting a success

,

• q, = probability of getting a failure

Identify in the problem our variables to replace in the distribution:

`\begin{gathered} n=25 \\ x=2 \\ p=0.09 \\ q=1-p \\ q=0.91 \end{gathered}`

Replace in the equation of the distribution:

`\begin{gathered} P(2)=(25!)/((25-2)!\cdot2!)\cdot(0.09)^2\cdot(0.91)^(25-2) \\ P(2)=\text{ }0.278 \end{gathered}`

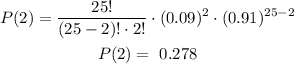
The probability that at most 2 are 65 or older is P(2)=0.278