The given problem can be exemplified in the following diagram:
Since we are told that "P" is a mid-point of DE, this means that:
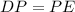
Also, since DE represents the entire segment, this means:
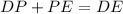
Therefore, we may replace the values of DP and PE as "6x + 4" and we also replace the given values of DE, we get:
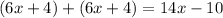
Adding like terms we get:

Now we solve for "x" first by subtracting 14x from both sides:
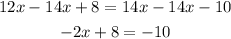
Now we subtract 8 from both sides:
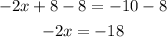
Now we divide both sides by -2:
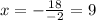
Therefore, the value of "x" is 9. Now we determine the length of DP using the expression for this segment:
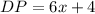
Replacing the value of "x":
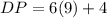
Solving the operations we get:
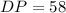
Therefore, the length of DP is 58 units.