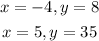ANSWER
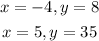
Step-by-step explanation
We want to find the values of x and y from the given system of equations:
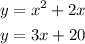
To do this, subsitute the second equation into the first:
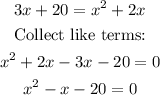
Now, solve by factorization:
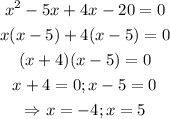
Now, substitute the values of x into the second equation to find the values of y:
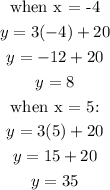
Therefore, the values of x and y are: