Consider a point (x,y) on the parabola.
Determine the distance between focus (0,-4) and point (x,y) by using the distance formula.
![\begin{gathered} d=\sqrt[]{(x-0)^2+(y-(-4))^2} \\ =\sqrt[]{x^2+(y+4)^2} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/dmd5533xn6z384z6m4p4a3g760fpmrgxhx.png)
Determine the distance between directrix y=4 and point (x,y).
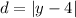
For the parabola distance between focus and point is equal to distance between directrix and point.
![\begin{gathered} \sqrt[]{x^2+(y+4)^2}=|y-4| \\ x^2+(y+4)^2=|y-4|^2 \\ x^2+y^2+8y+16=y^2-8y+16 \\ -16y=x^2 \\ y=-(x^2)/(16) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/naolr8op8w6qq59pvuiz4qr2bkn1fc0a3e.png)