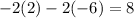Question

Find a solution to the linear equation −2x−2y=8 by filling in the boxes with a valid value of x and y.Provide your answer below:−2( )−2(. )=8

Answer 1

Given

`-2x-2y=8`

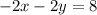
To find a solution for the linear equation, the first step is to write the equation in slope-intercept form:

-Pass the x-term to the right side of the equation by applying the opposite operation to both sides of the equal sign:

`\begin{gathered} -2x+2x-2y=8+2x \\ -2y=2x+8 \end{gathered}`

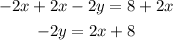
-Divide both sides by -2:

`\begin{gathered} (-2y)/(-2)=(2x)/(-2)+(8)/(-2) \\ y=-x-4 \end{gathered}`

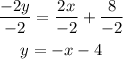
Once you have expressed the equation of the line in slope-intercept form, replace it with any value for x and calculate the corresponding value of y, for example, x=2

`\begin{gathered} y=-(2)-4 \\ y=-2-4 \\ y=-6 \end{gathered}`

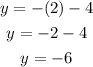
One solution for the linear equation is x=2 and y=-6, you can check the solution by replacing the values on the original equation, with both values the result should be 8:

`\begin{gathered} -2x-2y \\ -2\cdot2-2\cdot(-6) \\ -4+12=8 \end{gathered}`

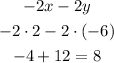
As you can see the values are a valid solution for the linear equation.

So the solution is:

`-2(2)-2(-6)=8`