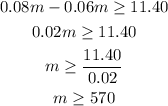Question

A phone company offers two monthly charge plans. In plan A, there is no monthly fee, but the customer pays 8 cents per minute of use. In plan B, the customer pays a monthly fee of $11.40 and then an additional 6 cents per minute of use. For what amounts of monthly phone use will plan A cost at least as much as plan B? Use m for the number of minutes of phone use in a month, and solve your inequality for m.

Answer 1

In plan A, the charge is

`8\text{cent per minutes with no monthly fe}e`

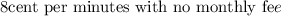
For Plan B, the company charge

`\text{ \$11.40 per month +6 cent per minutes }`

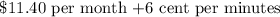
Since the Number of minutes is m

The amount of monthly phone use in plan A is

`\begin{gathered} \text{ 8m cent } \\ 0.08m\text{ dollar} \end{gathered}`

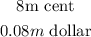
The amount of monthly phone use in plan B is

`\begin{gathered} \text{ \$11.40+0.06m} \\ \sin ce\text{ 100 cent=\$1} \\ 6\text{cent}=\text{ \$0.06} \end{gathered}`

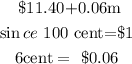
The amounts of monthly phone use of plan A cost at least as much as plan B

will be

`\begin{gathered} \text{The amount of Plan A }\ge\text{ The amount of plan B} \\ 0.08m\ge11.40+0.06m \end{gathered}`

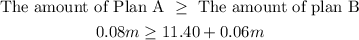
Then, by collecting like terms, we have

`\begin{gathered} 0.08m-0.06m\ge11.40 \\ 0.02m\ge11.40 \\ m\ge(11.40)/(0.02) \\ m\ge570 \end{gathered}`