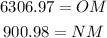As you can see the segments OM ME and OE form a right triangle. So to find the measure of the segment OM you can use the trigonometric ratio cos (θ):
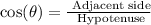
So, you have:
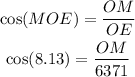
Angle MOE measures 8.13 ° because segment AO bisects angle NOE.
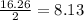
The measure of segment OE is 6371 because it is a radius of the circle just like segment AO.

Now, to find the measure of segment NM you can use the trigonometric ratio sin (θ):
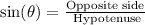
Also, the NM and ME segments are equal because the AO segment bisects the NOE angle. So, you have:
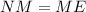

Therefore, the measurements of the OM and NM segments are: