Question

A square rock garden with sides of 120 feet is placed in the middle of a circular grass yard. If the circumference of the yard is 560 feet then how much area is covered by grass? For all calculations involving pi use 3.14 Hint: be careful that you do not do any rounding on answers until the very end of a problem part or you could create rounding error.A.) amount of area covered by grass, measured in square feet= ____ ft^2Round your answer to 2 decimal places as needed.B.) Amount of area covered by grass, measured in square yards = _____ yd^2Round your answer to 2 decimal places as needed.

Answer 1

In this case, we'll have to carry out several steps to find the solution.

Step 01:

Data:

square rock garden:

side = 120 ft

circular grass yard:

circumference = 560 ft

Step 02:

area (covered by grass):

area rock garden:

area (rg) = s² = (120 ft)² = 14400 ft²

area circular yard:

area (cy) = π r²

circumference = 2 π r

560 = 2 * 3.14 * r

560 / ( 2 * 3.14) = r

89.17 ft = r

area (cy) = 3.14 * (89.17 ft)² = 24967.05 ft²

area (covered by grass) = area (cy) - area (rg) = 24967.05 ft² - 14400 ft²

area (covered by grass) = 10567.05 ft²

area (covered by grass) (square yards):

`\text{area = 10567.05ft}^2\cdot(0.11yd^2)/(1ft^2)=1162.38yd^2`

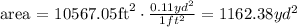
The answer is:

area (covered by grass) = 10567.05 ft²

area (covered by grass) = 1162.38 yd²