We can add the two similar terms on the right side of the inequality:
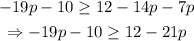
now we can move all the terms with p to the left side of the inequality, and all the constants to the right side:
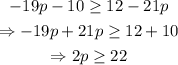
since the coefficient of the term 2p is positive, we can move it to the opposite side dividing without changing the inequality sign:
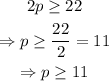
therefore, p is greater or equal to 11