1. Given:
Standard deviation: σ = 17.9
Confidence = 99%
Now, formula to find the margin of error is:
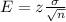
Where:
E is margin of error
z is critical value at confidence level
σ is standard deviation
n is required sample size
Since that the sample mean is within one-half year of the population mean. So:
E = 0.5
We have that z value at 99% Confidence level is z = 2.576.
We clear n in the formula:
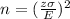
Substitute the values:
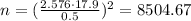
Round to the nearest whole number is 8505
Answer: The required sample size is 8505
2. Statistics students are younger than people in the general population. Therefore:
Answer: C.