Question

I only need help with question 5! i’ll provide the answer to question 4 if it helps with question 5

Answer 1

Given that slope =0.06.

The triangle is a right-angled triangle with base x and height y.

Here r is the length of the deck of the bridge.

y=the exact rise of the bridge.

x= the run of the bridge,

`\text{Slope =}(y)/(x)=0.06`

`\text{Slope =}(y)/(x)=(6)/(100)=(3)/(50)`

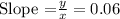
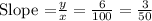
By using the Pythagorean theorem, we get the length r as follows.

`r=\sqrt[]{x^2+y^2}`

Substitute x=50 and y=3, we get

`r=\sqrt[]{50^2+3^2}=\sqrt[]{2500+9}=\sqrt[]{2509}=50.089`

The length of the bridge is 50.09.