Question

A hiker walks 23.87 m, E and 12.90 m, N. What is the direction of his resultantdisplacement?

Answer 1

23.38 ° to the positive x-axis

Step-by-step explanation

Step 1

draw the vectors

Step 2

add the vectors, ( component to component)

so

a) get the components of V1

`\begin{gathered} 23.87\text{ at 0\degree} \\ so \\ V_(1x)=23.87\text{ cos 0=23.87} \\ V_(1y)=23.87\text{ sin 0= 0} \end{gathered}`

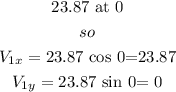
b) components of V2

`\begin{gathered} 12.9\text{ at 90 \degree} \\ so \\ V_(2x)=\text{ 12.9 cos 90=0} \\ V_(2y)=12.9\text{ sen 90=12.9} \end{gathered}`

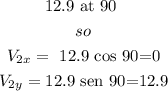
c) add

`\begin{gathered} Vdis_x=23.87+0=23.87 \\ Vdis_y=0+12.9 \end{gathered}`

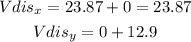
so, the magnitude of the displacement is

`\begin{gathered} \lvert Vd\rvert=\sqrt[]{V^2_x+V^2_y} \\ replace \\ \lvert Vd\rvert=\sqrt[]{23.87^2+12.9^2} \\ \lvert Vd\rvert=27.132 \end{gathered}`

finally, the direction

as we have a rigth triangle

let

opposite side= 12.9

adjacent side=23.8

Now, use the tan function to find the angles

so

`\begin{gathered} \tan \emptyset=\frac{opposite\text{ side }}{\text{adjancent side}} \\ \text{replace} \\ \tan x=(12.9)/(23.87) \\ \text{isolate x} \\ x=\tan ^(-1)((12.9)/(23.87)) \\ x=28.38 \end{gathered}`

therefore, the direction of the resultant is

23.38 ° to the positive x-axis

I hope this helps you