Question

Hey, I would appreciate it if you can help me with these problems, been stuck on it for a few days

Answer 1

Read below.

Explanation:

The formula for the average rate of change is:

`(f(b) - f(a))/(b - a)\\\\\textsf{Divide the change in y-values \big($f(b)$ and $f(a)$\big) by the change in x-values \big($b$ and $a$\big).}`

Given coordinates as a table:

`\begin{array} c \cline{1-2} \sf Elapsed\:Time\:(hours) & \sf Distance\:Traveled\:(miles)\\ \cline{1-2} 1 & 40\\ \cline{1-2} 2 & 110\\ \cline{1-2} 4 & 180\\ \cline{1-2} 6 & 230\\ \cline{1-2} 8 & 350\\ \cline{1-2} 10 & 390\\ \cline{1-2}\end{array}`

..................................................................................................................................................

Questions 1 - 4:

1) The first hour to the second hour:

`\boxed{\begin{minipage}{10.4 cm}$(f(b) - f(a))/(b - a) \implies (f(2) - f(1))/(2 - 1) \implies (100 - 40)/(2 - 1) \implies (70)/(1) \implies \boxed{70}$\end{minipage}}`

2) The second hour to the fourth hour:

`\boxed{\begin{minipage}{10.4 cm}$(f(b) - f(a))/(b - a) \implies (f(4) - f(2))/(4 - 2) \implies (180 -110)/(4 - 2) \implies (70)/(2) \implies \boxed{35}$\end{minipage}}`

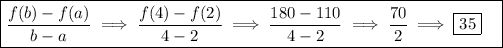
3) The sixth hour to the eighth hour:

`\boxed{\begin{minipage}{10.4 cm}$(f(b) - f(a))/(b - a) \implies (f(8) - f(6))/(8 - 6) \implies (350 - 230)/(8 - 6) \implies (120)/(2) \implies \boxed{60}$\end{minipage}}`

4) The eighth hour to the tenth hour:

`\boxed{\begin{minipage}{10.4 cm}$(f(b) - f(a))/(b - a) \implies (f(10) - f(8))/(10 - 8) \implies (390 - 350)/(10 - 8) \implies (40)/(2) \implies \boxed{20}$\end{minipage}}`

..................................................................................................................................................

Questions 5 - 7:

5) Looking at the calculations that have been done, we can see that their average speed was the greatest during the first to second hour.

6) Again, we can see that their average speed was the least during the eighth to tenth hours.

7) The average rate of change from the first to tenth hour is 38.9.

`\boxed{\begin{minipage}{10.6 cm}$(f(b) - f(a))/(b - a) \implies (f(10) - f(1))/(10 - 1) \implies (390 - 40)/(10 - 8) \implies (350)/(9) \implies \boxed{38.9}\ $\end{minipage}}`