Question

I need with a four part question to one problem

Answer 1

ANSWER and EXPLANATION

(a) The vertex form of a quadratic function is:

`f(x)=a(x-h)^2+k`

where (h, k) = vertex

a = leading coefficient

A graph opens up if the leading coefficient of the function is positive (greater than 0) and it opens downwards when the leading coefficient is negative (less than 0).

The leading coefficient of the given function is 5.

Hence, it opens upward.

(b) To find the vertex of the graph, we can compare the given function to the general vertex form of a quadratic function.

Doing that, we see that:

`(h,k)=(-2,4)`

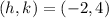
Hence, the vertex is:

`(-2,4)`

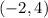
(c) The domain of a function is the set of all the x values of the function i.e. the set of all the input values of the function.

Hence, the domain of the function is:

`(-\infty,\infty)`

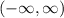
(d) The range of a function is the set of all y-values of the function i.e. the set of all output values of the function.

The vertex of the function is the minimum value of the function (since it opens up).

This means that the y-coordinate of the vertex is the least value in the range.

Hence, the range of the function is:

`\lbrack4,\infty)`

(e) To graph the function, we have to use another point asides from the vertex.

Let us find the value of the function at x = -1:

`\begin{gathered} f(-1)=5(-1+2)^2+4 \\ f(-1)=5(1)^2+4=5+4 \\ f(-1)=9 \end{gathered}`

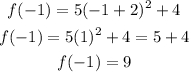
Hence, the second point is (-1, 9)

Now, let us plot the graph of the function:

That is the graph of the function.