Given data:
Length of peldulum is,
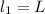
Period of pendulum is,
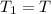
New period of pendulum is,
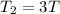
Formula:
Formula of period of pedulum is as follows:
![T=2\Pi\sqrt[]{(l)/(g)}](https://img.qammunity.org/2023/formulas/physics/college/57h1imewzd6ipsk7de8u9evrxzsrx5cum1.png)
For old period of pendulum above equation becomes as follows:
![T=2\Pi\sqrt[]{(L)/(g)}](https://img.qammunity.org/2023/formulas/physics/college/zexdae467akfggarjg7rzb89q34rqgjlk9.png)
Taking square of above equation,
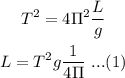
Now, for new period of pendulum,
![T_2=2\Pi\sqrt[]{(L_2)/(g)}](https://img.qammunity.org/2023/formulas/physics/college/iumq9k4gb741r11q0xt6fnaqeiddq0bsgh.png)
Taking square of above equation,
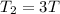
Hence,
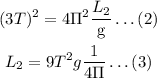
Taking ratio of equation-(3) and equation-(1),
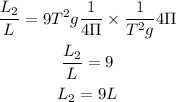
Therefore, Length of pendulum should be 9L for the period to be 3T seconds.