ANSWER and EXPLANATION
We want to first graph the function given for the domain (-2, 2).
That domain given means that x is between - 2 and 2.
So let us pick the points:
x = -2, -1, 0, 1 and 2
Therefore, we will find f(x) for those values:
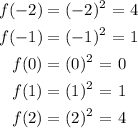
Now, let us graph it.
That is the graph of f(x) = x^2 in the domain (-2, 2)
Now, we have that g is obtained from f by translating it 2 units up.
Let us represent that in the graph by simply moving the graph of f(x) upwards with 2 units:
The red graph represents the graph of g(x).
For the equation of g(x), we know a translation is represented by a general formula:
g(x) = f(x - a) + b
where a = horizontal shift and b = vertical shift
In this case, there is only a vertical shift of 2 upwards and so we have that a = 0, b = 2
g(x) then becomes:
g(x) = f(x) + 2
