Given:
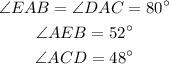
Now consider the triangle EAB and triangle CDA,
it is observed that,
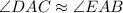
But no other angles are similar.
So, triangle EAB is not similar to triangle CDA
Similarly for, Triangle BAE and CAD, triangle AEB and ADC , triangle DCA and BAE only one angle is similar.
Hence, it is concluded that no triangles are similar.