Question

What is the equation of a line that is perpendicular to y = 3x-2 and passesthrough the point (6,8)?O A. y 3x+4O B. y=-3x+10O c. y - x + 6OD - x+8y =+8

Answer 1

For two lines to be perpendicular, the product of their slope must be equal to -1.

That is

`\begin{gathered} m1* m2=-1 \\ \text{Where m1 and m2 are the slopes of the lines } \end{gathered}`

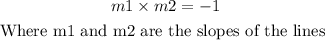
Equation of a line in slope-intercept form is given as

`\begin{gathered} y=mx+b \\ \text{where m is slope } \end{gathered}`

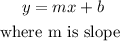
Comparing this to

`\begin{gathered} y=3x-2 \\ \text{the slope m1 = 3} \end{gathered}`

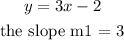
Now, let's find the slope of the other line m2.

`\begin{gathered} m1* m2=-1 \\ 3* m2=-1 \\ m2=(-1)/(3) \end{gathered}`

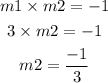
Now, equation of a line in point-slope form is

`y-y_1=m(x-x_1)`

Relating this to this second slope we have

`y-y_1=m2(x-x_1)`

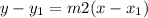
The equation becomes

`\begin{gathered} y-y_1=m2(x-x_1) \\ y-y_1=(-1)/(3)(x-x_1) \\ \text{from the point }\mleft(6,8\mright) \\ x_1=6,y_1=8 \\ \text{Hence } \\ y-y_1=(-1)/(3)(x-x_1) \\ y-8_{}=(-1)/(3)(x-6_{}) \\ y-8_{}=(-1)/(3)x+(6)/(3)_{} \\ y-8=(-1)/(3)x+2 \\ y=(-1)/(3)x+2+8 \\ y=(-1)/(3)x+10 \\ y=-(1)/(3)x+10 \end{gathered}`

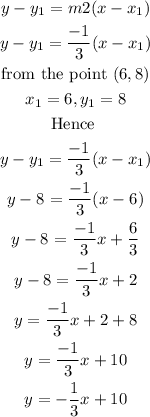
Hence, the answer is

`y=-(1)/(3)x+10`

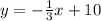
Option B