From the question,
We are given that the probability of a person being a dog-owner is 30%
Therefore,
The probability of a person not being a dog-owner is 70%
Hence
probability of success, p= 30%
Probability of failure, q = 70%
By binomial probability formula we have
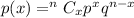
Part A
We are to find the probability of exactly 4 dog-owners if 10 dog owners are randomly selected
This implies
x = 4, n = 10
Applying the formula
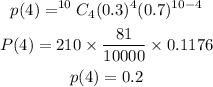
Therefore, the probability that exactly 4 own dogs is 0.2
Part B
We are to find the probability that at least 4 of them own dogs
at least 4 means 4 and above
Therefore
The probability of at least 4 will be
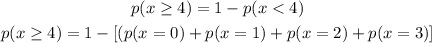
By substituting values we have

Hence, we have
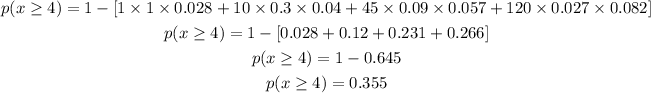
Therefore, the probability that at least 4 of them own dogs is 0.355