The lenght of the rectangle is increasing at the rate of 8in/sec while its width is decreasing at 3 in/sec. Find the rate of change of it's area when it's length is 75 in and width is 35in
Solution :
Let x be the length and y is the width of the rectangle
It is given that increase length of rectnagle is 8
i.e.,
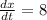
It is given that decrease width of rectangle is 3in/sec
i.e.,
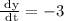
Area of rectangle is defined as the product of length and breadth
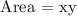
Differentiate the area with respect to time t;
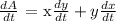
Substitute the value as x = 75 and y = 35 dx/dt = 8 and dy/dt = -3
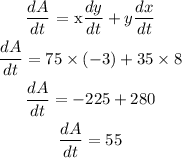
Rate of change of area is 55 unit square
;;;