SOLUTION
The diagram is represented below
We were told to find angle GCE. I have represented angle GCE as y.
Angles DCF and FCE make up a straight line. Sum of angles on a straight line = 180 degrees.
That means angle DCF + angle FCE = 180
therefore,
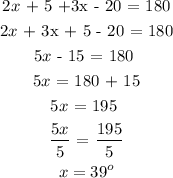
Now we have found the value for x, let us find angle GCE
Note that angle GCE is vertically opposite to angle DCF. Also vertically opposite angles are equal. Therefore DCF = GCE
GCE = DCF
y = DCF
y = 2x + 5
y = 2(39) + 5
y = 78 + 5 = 83 degrees.
Therefore, angle GCE = 83 degrees