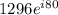Question

Use DeMoivre's Theorem to calculate the following expression. Write the exact answer in the form found using Euler's Formula, Izlell. Do not round. Make sure that !argument of your answer lies in the interval 0 , 360 ).[6(cos(110°) + isin(110*))J*

Answer 1

We are given the following expression

`[6(\cos(110\degree)+i\sin(110\degree))]^4`

We are asked to simplify the above expression using DeMoivre's Theorem.

Recall that DeMoivre's Theorem is given by

`[r(\cos\theta+i\sin\theta)]^n=r^n(\cos n\theta+i\sin n\theta)`

Let us apply the above theorem to the given expression

`[6(\cos(110\degree)+i\sin(110\degree))]^4\Rightarrow6^4(\cos(4\cdot110\degree)+i\sin(4\cdot110\degree))\Rightarrow1296(\cos(440\degree)+i\sin(440\degree)`

We know that 360° is a full rotation.

440° - 360° = 80°

`1296(\cos(80\degree)+i\sin(80\degree))`

Finally, let us write the above expression using Euler's Formula

`1296(\cos(80\degree)+i\sin(80\degree))\Rightarrow1296e^(i80)`

Therefore, the given expression has been simplified.

`1296e^(i80)`