Question

Use the Factor Theorem to determine whether x + 3 is a factor of P(x)=x⁴+x³-4x² +8. Specifically, evaluate P at the proper value, and then determine whether x + 3 is a factor. P() = 0 O x + 3 is a factor of P(x) O x + 3 is not a factor of P(x)

Answer 1

Given:

Use the Factor Theorem to determine whether x + 3 is a factor of P(x)=x⁴+x³-4x² +8.

Required:

Determine if x + 3 factor or not.

Step-by-step explanation:

We know by factor theorem that if f(a) = 0 for a polynomial then (x - a) is a factor of the polynomial f(x).

It means for (x + 3) to be factor f(-3) = 0

Now,

`\begin{gathered} P(x)=x^4+x^3-4x^2+8 \\ P(-3)=(-3)^4+(-3)^3-4(-3^)^2+8 \\ P(-3)=26 \end{gathered}`

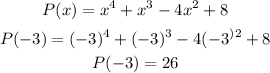
We get, P(-3) is not equal zero. So, (x + 3) is not a factor.

Answer:

x + 3 is not a factor of P(x).