SOLUTION
Write out the function
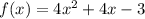
There are several ways of solving a quadratic equation. The quadratic formula, factorization, graphical method, etc.
Part A
To tell whether a quadratic equation is factorable, we use the Discriminant
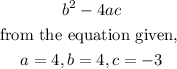
Hence
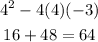
Since the discriminant is greater than zero and a perfect square hence, it is factorizable
Hence, there is more than one way to solve or determine the zeros of the function
Part B
To find the zeros of the function, we equate the f(x) to zero
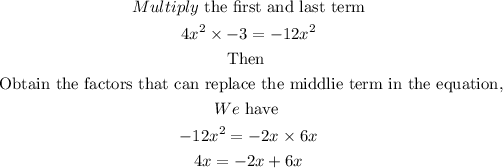
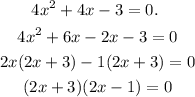
Then equate each of the factors to zero
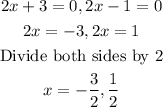
Therefore, the zeros of the function are
-3/2 and 1/2