Question

2. Write the equation of 9(.) given the table below. - 2 -1 3 6 1 12

Answer 1

Function Modeling

The table shows the relationship between the variable x and the function g(x).

We are given the values:

g(-2)=3

g(-1)=6

g(1)=12

We need to test if the table corresponds to a linear function

It can be done by calculating the slope between any two points. If the slope is constant for all the possible pair of points, then we are sure it's a linear function.

Given two points (x1,y1) and (x2,y2), the slope of the segment between them is calculated as:

`m=(y_2-y_1)/(x_2-x_1)`

Select the two first points (-2,3) and (-1,6). We have:

x1=-2, y1=3, x2=-1, y2=6. Substituting:

`m=(6-3)/(-1+2)=(3)/(1)=3`

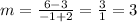
The slope is 3. Now try the last two points (-1,6) and (1,12):

`m=(12-6)/(1+1)=(6)/(2)=3`

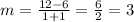
Since the slope is constant and has a value of 3, we are certain the function g(x) is a straight line.

Now find the equation of g(x). Let's call y=g(x)

The point-slope form of the line passing through the point (h,k) and with slope m is:

y - k = m( x - h )

Select any point form the table, for example: (1,12) and substitute into the formula:

y - 12 = 3( x - 1 )

Operating:

y - 12 = 3x - 3

Adding 12:

y = 3x + 9

Thus, the equation of g(x) is:

g(x) = 3x + 9