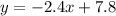Question

Find the equation of the line tangent to the graph of the function…

Answer 1

Given the equation:

`w(x)=(15)/(x^2+1)`

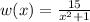
Let's find the equation of the line tangent to the graph of the given function at the point (2, 3)

Let's find the first derivative and evaluate for the values at x = 2, y = 3.

We have:

Differentiate w(x) using Constant Multiple rule

`\begin{gathered} 15(d)/(dx)\lbrack(1)/(x^2+1)\rbrack \\ \\ =15(d)/(dx)\lbrack(x^2+1)^(-1)\rbrack \end{gathered}`

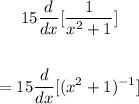
Next is to differentiate using chain rule:

Rewrite u for (x²+1)

`\begin{gathered} 15((d)/(du)\lbrack u^(-1)\rbrack(d)/(dx)\lbrack x^2+1\rbrack) \\ \\ =15(u^(-2)(d)/(dx)\lbrack x^2+1\rbrack) \\ \\ =15(-(x^2+1)^(-2)(d)/(dx)\lbrack x^2+1\rbrack) \\ \\ =-15(x^2+1)^(-2)(2x+0) \\ \\ =-30(x^2+1)^(-2)x \\ \\ =(-30x)/((x^2+1)^2) \end{gathered}`

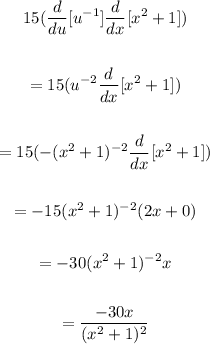
Now, evaluate the derivative when x = 2.

Substitute 2 for x and evaluate:

`\begin{gathered} (-30(2))/((2^2+1)^2) \\ \\ =(-60)/((4+1)^2) \\ \\ =(-60)/((5)^2) \\ \\ =(-60)/(25) \\ \\ =-2.4 \end{gathered}`

Thus, the slope of the tangent line is -2.4.

Apply the point-slope form of a linear equation:

y - y1 = m(x - x1)

Where m is the slope.

Input the values of (2, 3) for x1 and y1. Then substitute -2.4 for m:

`y-3=-2.4(x-2)`

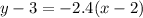
Let's solve the euqtion for y.

Apply distributive property to right side of the equation:

`\begin{gathered} y-3=-2.4x-2.4(-2) \\ \\ y-3=-2.4x+4.8 \end{gathered}`

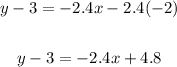
Add 3 to both sides of the equation:

`\begin{gathered} y-3+3=-2.4x+4.8+3 \\ \\ y=-2.4x+7.8 \end{gathered}`

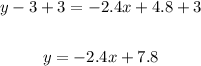
Therefore, the equation of the line tangent to the graph of the given function is:

y = -2.4x + 7.8

ANSWER:

`y=-2.4x+7.8`