Question

The polygons are similar, but not necessarily drawn to scale. Find the value of x.A) x=13B) x=7C) x=10D x=5.5

Answer 1

The polygons are similar, this means that we can find a conversion factor or scale factor between the polygons.

The scale factor will be the number by which we need to multiply the measures of the sides on the smaller polygon to get the measure of the sides of the larger polygon.

We find the scale factor by dividing the measure of one side of the larger polygon by the measure of one side of the smaller polygon (the sides has to be the corresponding sides), for example, since the side of 8 (in the larger polygon) is corresponding to the side of 2 (in the smaller polygon), we divide them:

`\begin{gathered} \text{scale factor=8/2} \\ \text{scale factor =4} \end{gathered}`

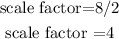
we can also use the corresponding sides of 16 (larger polygon) and 4 (smaller polygon) to see that we get the same scale factor:

`\begin{gathered} \text{scale factor=16/4} \\ \text{scale factor =4} \end{gathered}`

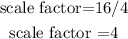
Now, we need to find the value of x.

First, we find the corresponding side to the side "x-3":

The sides marked in red are corresponding sides.

As we said, the scale factor is the number by which we need to multiply the measures of the smaller polygon to get the measure of their corresponding side in the larger polygon:

So, by multiplying 2.5 by 4 we should get x-3:

`2.5*4=x-3`

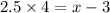
2.5 by 4 is 10:

`10=x-3`

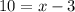
Finally, to solve this equation, add 3 to both sides to find x:

`\begin{gathered} 10+3=x-3+3 \\ 13=x \end{gathered}`

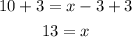
Answer: x=13