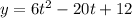Question

Construct parametric equations describing the graph of the following equation.y = 6x2 + 4x - 4If x = 1 - 2, find the parametric equation for y.

Answer 1

The parametric equation for y is:

`y=6t^2-20t+12`

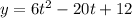
Step-by-step explanation:

To solve this problem, given x = t-2, we replace this value in the original equation.

The original expression is:

`y=6x^2+4x-4`

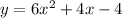
Then, x = t - 2:

`y=6(t-2)^2+4(t-2)-4`

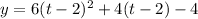
Now, we can develop the squared binomial, and apply distributive property in the second parentheses:

`y=6(t^2-4t+4)+4t-8-4`

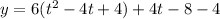
Apply distributive property in the parentheses:

`y=6t^2-24t+24+4t-12`

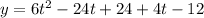
And solve the sums and rests:

`y=6t^2-20t+12`