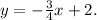Question

Use the information given to find the equation of the line using the point-slope formula (y – y_1) = m(x – x_1). Then convert your answer to slopeintercept form (y = mx + b).y-intercept of 2 and (4,-1)

Answer 1

Using the formula for the slope of a line that passes through two given points we get:

`\begin{gathered} m=(-1-2)/(4-0), \\ m=(-3)/(4), \\ m=-(3)/(4)\text{.} \end{gathered}`

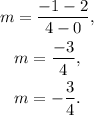
Now, using the point-slope formula for the equation of a line we get:

`y-(-1)=-(3)/(4)(x-4)\text{.}`

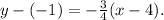
Taking the above equation to its slope-intercept form we get:

`\begin{gathered} y+1=-(3)/(4)x-(3)/(4)(-4), \\ y=-(3)/(4)x+3-1, \\ y=-(3)/(4)x+2 \end{gathered}`

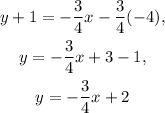
Answer:

The point-slope form is:

`y-(-1)=-(3)/(4)(x-4)\text{.}`

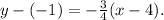
The slope-intercept form is:

`y=-(3)/(4)x+2.`