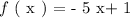SOLUTION:
Step 1:
In this question, we are meant to find the equation of the line passing through the given points:
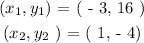
Step 2:
First, we need to calculate the gradient of the two points:
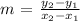
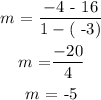
Step 3:
Using the formulae:
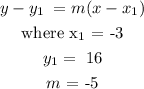
Putting the values into the equation, we have that:

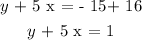
CONCLUSION:
The function notation to write the equation is given as:

since y = f ( x ), then