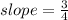
Step-by-step explanation
Slope describes the steepness of a line. The slope of any line remains constant along the line.to find the slope we need to apply the formula
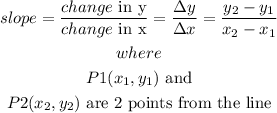
Step 1
a) pick up 2 points from the line ( the indicated points in the graph)
let
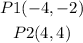
b) now, replace and evaluate
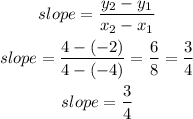
so, the slope of the line is 3/4
I hope this helps you